Learning geometry-based robot-manipulation skills
In many robot control problems, skills such as stiffness, damping and manipulability ellipsoids are naturally represented as symmetric positive definite (SPD) matrices, orientations are represented as unit quaternions, sensory data processed as spatial covariances, etc., which capture the specific geometric characteristics of those skills. Typical learned skill models such as dynamic movement primitives (DMPs), probabilistic learning algorithms, kernelized movement primitives, etc., can not, be directly employed with quantities expressed as SPD or unit quaternion as they are limited to data in Euclidean space. These skills demand special treatment using geometric methods based on Riemannian manifolds.
In this line of research, we investigate ways to develop new algorithms capable of learning and adapting geometry-form robot manipulation skills by exploiting metric learning approaches in order to build a Riemannian manifold of skill instances or tasks.
People involved
- Fares J. Abu-Dakka (fares.abu-dakka@aalto.fi), Research Fellow
Project updates
User-friendly virtual reality learning from demonstration setup
During the 2022 AEE Project Work course the students Eetu Suominen, Sampo Vänninen, Emrehan Öz and Nico Renlund developed and built a virtual reality learning from demonstration (LFD) setup in our lab.
Accepted papers!!!
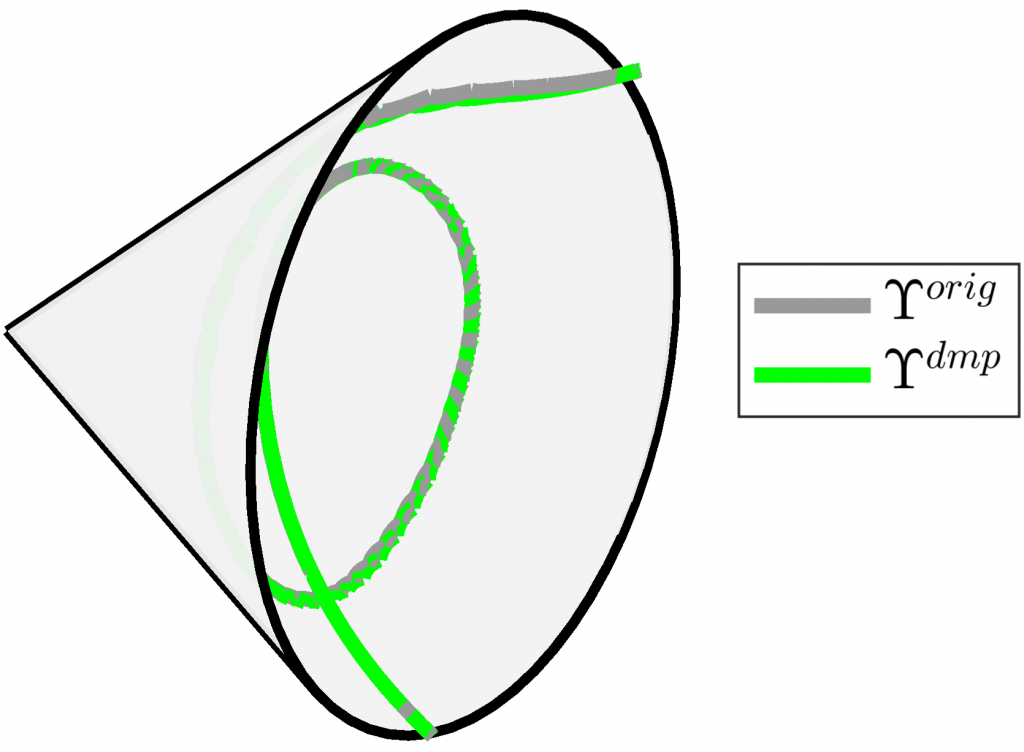
Great news!!! Our paper on “Geometry-aware Dynamic Movement Primitives” got accepted in ICRA2020