Accepted papers!!!
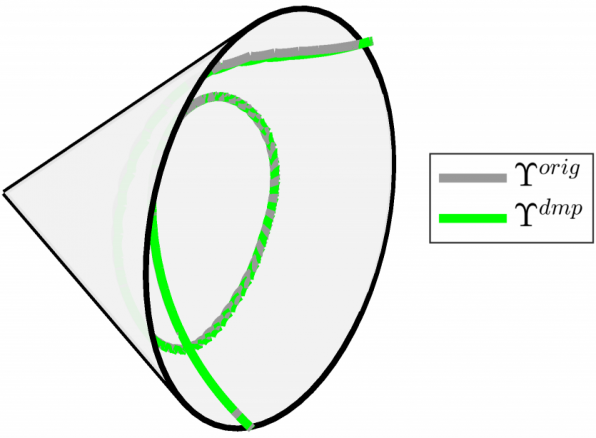
Great news!!! Our paper on “Geometry-aware Dynamic Movement Primitives” got accepted in ICRA2020
Abstract— In many robot control problems, factors such as stiffness and damping matrices and manipulability ellipsoids are naturally represented as symmetric positive definite (SPD) matrices, which capture the specific geometric characteristics of those factors. Typical learned skill models such as dynamic movement primitives (DMPs) can not, however, be directly employed with quantities expressed as SPD matrices as they are limited to data in Euclidean space. In this paper, we propose to use Riemannian metrics to reformulate DMPs such that the resulting formulation can operate with SPD data in the SPD manifold. Evaluation of the approach demonstrates that beneficial properties of DMPs such as change of the goal during operation apply also to the proposed formulation.